El Solucionador (también denominado Solver, por su nombre en inglés)es una forma más elaborada de búsqueda de soluciones que la Búsqueda del valor destino.
El Solucionador permite resolver planteamientos con las siguientes características:
- Puede utilizar múltiples variables (no sólo una, como ocurre con Búsqueda del valor destino)
- Admite la maximización o minimización del resultado (no tan sólo que adopte un valor determinado).
- Admite restricciones, un conjunto de normas que definen si alguna variable debe ser mayor, menor o igual a determinado valor. También se pueden definir restricciones para que una variable sea un valor entero (sin decimales) o binario (sólo 0 o 1).
De manera predeterminada Calc es suministrado con un Solucionador de programación lineal solamente. Esto optimiza los modelos en cierta medida. Sin embargo, con fórmulas más complejas o restricciones, es necesario la programación no lineal. Esa limitación queda cubierta por la extensión Solucionador para Programación no-lineal instalada por defecto con el programa. Esta extensión incorpora dos Algoritmos Evolutivos que pueden manejar variables de punto flotante y entero, así como las restricciones no lineales.
Veamos un ejemplo de su uso. Podemos reproducir los pasos de su resolución descargando el archivo solver-vehículos.ods.
Enunciado del problema
Una cadena de montaje de vehículos es capaz de montar hasta 80.000 vehículos al mes de dos tipos diferentes, A y B. Los gastos de producción de cada vehículo del tipo A ascienden a 5.400 €. y los del tipo B a 3.400 €. Los gastos totales de producción al mes no han de superar los 36 millones de euros. La ganancia neta es de 1.200 € por cada coche de tipo A y de 900 € por cada uno del tipo B.
¿Cuántos vehículos de cada tipo conviene fabricar cada mes para que la ganancia sea máxima?
Calcular la solución con el Solucionador
Este tipo de problemas se pueden diseñar de diferentes maneras en la hoja de cálculo. Hemos optado por plantearlo del siguiente modo.
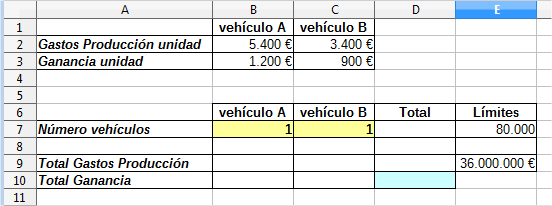
Están sombreadas en amarillo las celdas variables que se pretenden resolver, es decir, el Número vehículos de cada tipo a fabricar. Para usar el Solucionador es conveniente usar valores razonables para las variables de entrada, pues de lo contrario podrían distorsionar el cálculo y no encontrar una solución óptima. Por eso, rellenaremos estas celdas con el valor de 5.000 vehículos de cada tipo.
Completaremos las fórmulas para obtener los totales de Gastos de Producción y de Ganancia, multiplicando los correspondientes valores unitarios por el número de vehículos, para los dos tipos de vehículos.
La columna D la completaremos con la suma de Número vehículos, Total Gastos Producción y Total Ganancia de ambos tipos de vehículo.
Hemos usado la columna E para establecer los límites que nos plantea el enunciado.
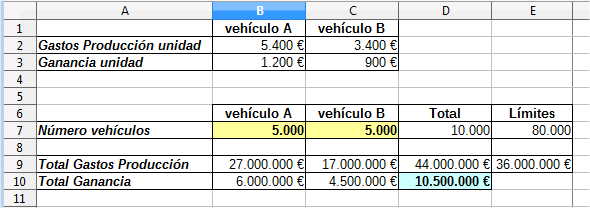
Podemos observar a simple vista, que no es posible fabricar 5.000 vehículos de cada tipo, porque excederemos el límite que tenemos para los Gastos de Producción. No importa, el solucionador se encargará de calcular los valores adecuados.
No situaremos en la celda que pretendemos optimizar, la suma de ganancias total (D3, sombreada en azul) y activaremos el menú Herramientas > Solucionador, que nos mostrará el diálogo Solucionador.
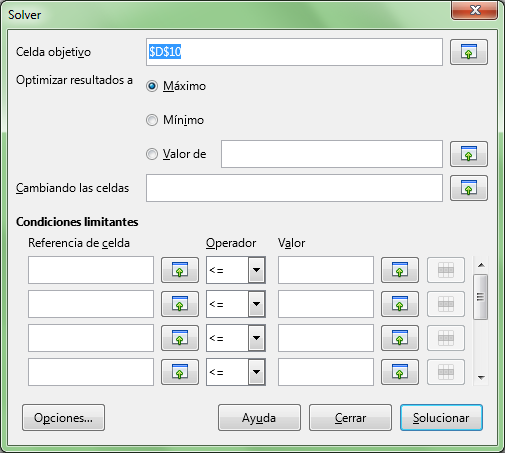
Podemos comprobar que todos los campos del diálogo que admiten referencias a celdas disponen del botón Encoger para poder facilitar su selección.
La Celda objetivo ya está cumplimentada por la referencia a la celda desde la cual llamamos al diálogo. Si no fuese la correcta, la podríamos seleccionar ahora.
El apartado Optimizar resultados a, nos permite determinar Máximo, Mínimo, o un Valor de específico (aquí podríamos introducir un valor o una referencia a una celda). En nuestro caso, se trata de obtener la ganancia máxima, así que dejaremos activada la opción Máximo.
En Cambiando las celdas introduciremos las celdas variables. En el ejemplo, $B$7:$C$7
A continuación tenemos el apartado Condiciones límites, donde añadiremos todo el conjunto de restricciones. Cada restricción está compuesta por:
- una Referencia de celda
- un Operador (<=, =, >=, entero o binario)
- un Valor (que puede introducirse directamente o mediante referencia a una celda)
Veamos las restricciones que debemos aplicar para nuestro ejemplo:
- el total de vehículos fabricados no puede ser superior a 80.000: $D$7 <= $E$7.
- el total de gastos de producción no puede ser superior a 36 millones: $D9 <= $E$9.
Hay algunas restricciones más que fácilmente se nos pueden pasar por alto:
- una solución matemática, puede decidir que deberíamos fabricar "medios vehículos" o "tres cuartos de vehículo", lo que evidentemente no es la solución deseada, por eso estableceremos que la cantidad de vehículos para cada tipo es entera: $B$7 Entero y $C$7 Entero.
- otra solución matemática podría decidir que de uno de los tipos de vehículos hemos de fabricar "menos mil unidades", lo cual es ilógico. En algún sitio hemos de informar al Solucionador de que la cantidad de vehículos de cada tipo es positiva y no puede ser negativa. Pero eso no lo haremos mediante restricciones, sino desde el botón Opciones que exploraremos seguidamente.
Hasta este punto, ya hemos completado los datos principales del modelo como se muestra en la imagen.
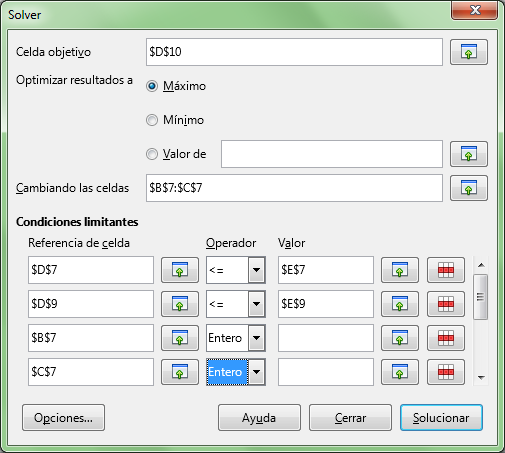
Para completar los parámetros de la solución, pulsaremos al botón Opciones.
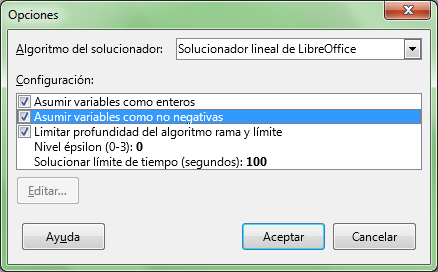
En el diálogo de Opciones podremos escoger entre los diferentes motores de cálculo que incorpora Calc. Cada uno de ellos dispone de diferentes opciones de Configuración.
En principio recomendamos usar el más sencillo: Solucionador lineal de LibreOffice, pero para cierto tipos de problemas no será el más adecuado, en cuyo caso podemos explorar los otros, aunque sus opciones de configuración requieren conocimientos matemáticos avanzados.
Advertencia
Algunos de los algoritmos de cálculo para el Solucionador que se instalan con LibreOffice, exigen una correcta instalación del JRE (Java Runtime Environment). Si no tienes Java en tu ordenador, o no estás seguro del que necesitas, visita la web de Java en http://java.com desde donde podrás descargarlo.
No obstante, algunas opciones si que son bastante intuitivas. En el caso que hemos seleccionado:
- Asumir variables como enteros (ya lo habíamos añadido como restricción, pero dado que el propio algoritmo del Solucionador lo tiene previsto, lo activaremos también aquí).
- Asumir variables como no negativas (el caso que comentábamos anteriormente) también lo activaremos.
Después de aceptar las opciones y pulsar el botón Solucionar, tras una breve pausa, se mostrará la solución:
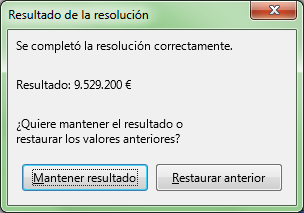Pulsando el botón Manetener resultados, la solución se insertará en las celdas variables de la hoja de cálculo.
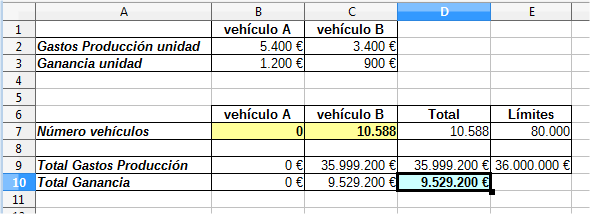
En este caso, la solución encontrada nos indica que deberíamos aplicar todos nuestros recursos a fabricar todas las unidades posibles del vehículo de tipo B, concretamente 10.588 unidades.
Este ejemplo ha sido muy sencillo, y posiblemente no hubiésemos necesitado del Solucionador para llegar a esta respuesta, pero podemos complicarlo con restricciones adicionales. Por ejemplo, podemos plantear que hay una necesidad comercial de fabricar ambos tipos de vehículos y que, como mínimo, hay que fabricar un 30% de cada uno de ellos. ¿Cómo modificaremos el modelo y las restricciones para encontrar la solución en este caso? Dejamos esta cuestión para su investigación personal.
Como podemos ver, el Solucionador puede ser una herramienta muy útil para varios tipos de problemas: necesidades logísticas, asignación de recursos o planificación publicitaria, entre otras.