En diferentes ocasiones podemos vernos en la necesidad de evaluar simultáneamente diferentes condiciones lógicas, para comprobar si se cumplen todas o sólo alguna de ellas, así como también comprobar la negación de una expresión lógica.
Para ello disponemos de estas funciones NO(), Y(), O().
O tomar decisiones, evaluando una pregunta y actuando de una forma si la respuesta es VERDADERO, o de otra si es FALSO. Para tomar decisiones disponemos de la función SI().
Función SI()
SI permite obtener un valor u otro en función de una expresión lógica dada.
Sintaxis básica:
=SI(Expresión_lógica;[Valor_si_VERDADERO];[Valor_si_FALSO])
donde:
- Expresión_lógica es la condición o comparación que se desea evaluar
- Valor_si_VERDADERO es el resultado que devolverá la función si la Expresión_lógica se resuelve como VERDADERO. Este argumento es opcional; de omitirlo, la función devolverá VERDADERO.
- Valor_si_FALSO es el resultado que devolverá la función si la Expresión_lógica se resuelve como FALSO. Este argumento es opcional; de omitirlo, la función devolverá FALSO.
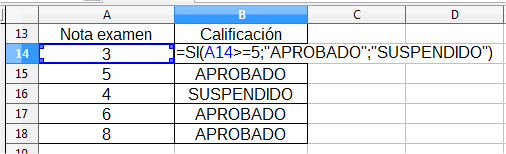
En los siguientes ejemplos se muestra el texto APROBADO si la nota del examen es igual o superior a 5 o SUSPENDIDO en caso contrario.
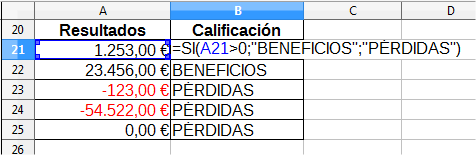
La función SI() tiene una limitación y es que al ser tan binaria, para ella somos bajos o altos, gordos o delgados, blancos o negros, pues sólo nos da a escoger entre dos opciones. Y la vida real tiene muchos más matices. Veamos un ejemplo tan sencillo como el anterior, en que a continuación de unos resultados económicos se muestra el término BENEFICIOS o PÉRDIDAS en función de los mismos. ¿Qué ocurre cuando el resultado es exactamente cero?
A todos nos consta que un resultado cero no representa beneficios de ningún tipo, pero tampoco podemos afirmar que se trate de pérdidas. En un caso así, necesitaríamos una tercera opción, NULO o algo parecido para poder calificar correctamente. Ahí es donde entra en juego el anidamiento de funciones. Después de comprobar que el resultado no es mayor que cero, quedan dos posibilidades: que sea igual a cero o que sea menor que cero. Por consiguiente, sustituiremos el tercer argumento de la función SI(), por otra función SI() que evalúe esta segunda expresión. En el caso del ejemplo...
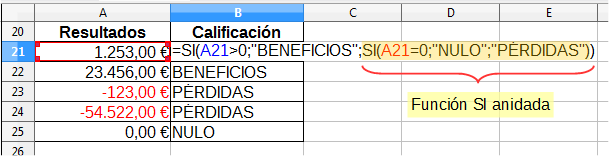
Hemos sombreado la función anidada para facilitar su lectura.
Por tanto, podemos deducir que para evaluar dos opciones, basta con una función SI(), para evaluar más opciones, necesitaremos una nueva función SI() por cada nueva opción.
El incremento de funciones anidadas puede convertir la fórmula en algo inmanejable, proclive a errores difíciles de depurar. Por eso, si vemos que necesitamos un excesivo número de funciones SI anidadas, comprobaremos en el próximo apartado que, con una pequeña modificación de enfoque, podemos resolver el problema con extrema sencillez usando la función BUSCARV.
Función NO()
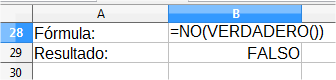
NO invierte el valor lógico del argumento.
Sintaxis básica:
=NO(Expresión_lógica)
Función Y()
Y devuelve VERDADERO, si todos los argumentos son VERDADERO; en cualquier otro caso, devuelve FALSO.
Sintaxis básica:
=Y(Expr_lógica1;[Expr_lógica2];...)
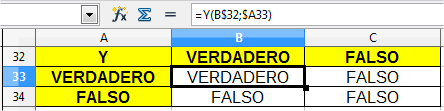
En el ejemplo, una tabla de la verdad de la función Y.
Función O()
O devuelve FALSO, si todos los argumentos son FALSO; en cualquier otro caso, devuelve VERDADERO.
Sintaxis básica:
=O(Expr_lógica1;[Expr_lógica2];...)
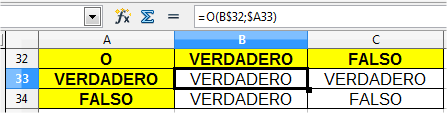
En el ejemplo, una tabla de la verdad de la función O.